What if I told you there was a problem that if you solved you would get over one billion dollars? That problem exists, and if you're smart enough, you may just be able to cash in, but more on that in just a bit.
Let's start with something easier, multiplication. What's 5 times 7? Not a trick question, it's pretty easy right? It's 35. What if I asked you to multiply together 13 and 17, could you do it? You can use a calculator, but I think to illustrate my point better, maybe try and do it by hand. Did you get the answer? It's 221. Alright, what if I asked you to multiply 127 and 131? It's starting to get a little harder, but still if you had paper in front of you and a minute or so, I'm guessing you would be able to find the answer which is 16,637. This problem is certainly getting trickier as I add more digits, but it's not getting impossibly difficult, and I'm guessing if I told you I'd give you a billion dollars for it you'd be able to solve it.
What about doing the reverse of this? If I asked you, "What are the two prime factors of 1003?" How would you even go about solving this? A naive approach might be to just try all the odd numbers between 3 and the square root of 1003. Is it divisible by 3? No, 5? no, and so on. But what if I told you that the answer was 17 * 59? You could verify whether or not that was the correct solution really quickly.
Alright, now for a harder one. What are the two prime factors of 50,867,977? If you don't have a computer this would probably take you a week to solve. Okay, but what if I told you that the answer was 6,827 * 7,451? You could just punch that into your calculator, and hey, look at that, that's the answer! As the two numbers get larger and larger, multiplying them together gets slightly harder, but doing the reverse, finding the two prime factors from the product, gets incredibly more difficult. So why is it so much easier to verify whether an answer is correct compared to actually finding the answer? The answer is because you know a very good algorithm for multiplying numbers together, but you don't know an equally fast algorithm for factoring a number. In fact, no one does, at least not yet* (ignoring Shor's Algorithm using quantum computers). So is something about factoring fundamentally more difficult than multiplying? This question isn't worth a billion dollars, it's only worth one million. It's essentially the computer science problem known as P versus NP, that is, does there exist a classification of problems which are verifiable in polynomial time (multiplying two numbers together), but only solvable in non-polynomial time (factoring numbers)? Or put more simply, is factoring actually more difficult than multiplying (P != NP) or are we all just collectively dumb and haven't thought up a good way to do it yet (P == NP). If you can answer this question you will go down as the greatest computer scientist to ever live, and the Clay Mathematics Institute will award you one million dollars.
But wait, you told me I could get one billion dollars? My time is valuable!
Alright, let's move on to something that's a little less intuitive, but fairly analogous. That is, elliptic curve cryptography and the discrete log problem.
Let's start by defining what an elliptic curve is. An elliptic curve is just a curve modeled by an equation in the form y2 = x3 + ax + b. It has an interesting property that it's symmetrical about the x-axis, which if you think about it makes sense, since if I take the square root of both sides I get y = +/- √ (x3 + ax + b). One elliptic curve which has gotten a lot of attention is y2 = x3 + 7. It's not particularly special, though it does have an interesting property, one that is shared by infinite other elliptic curves though, that for any given x value, one y value will be positve and one will be negative. This lets us define any particular point by only its x value and a single bit known as the y-parity to denote if we're talking about the positive y point or the negative. This curve is known as Secp256k1 and it's the curve used by many cryptocurrencies such as Bitcoin and Ethereum.
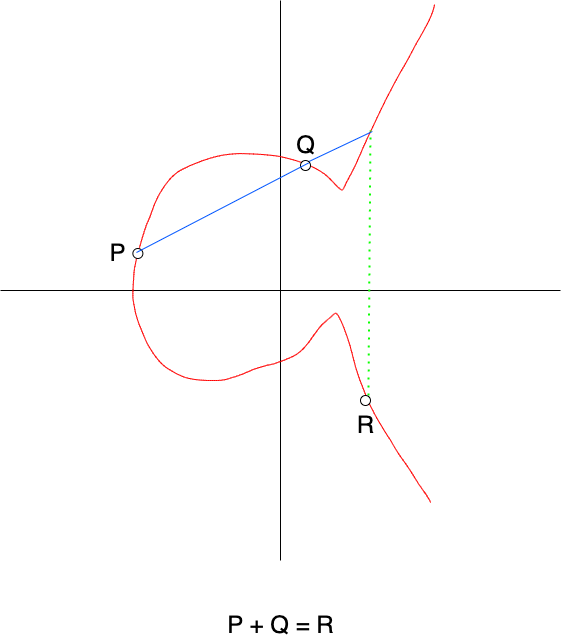
Okay, so I get it, you want that billion dollars, well, you're almost there. One thing first though, you do need to learn how to add points on an elliptic curve. Just like you can add two numbers together, you can also add up two points on an elliptic curve. How do you do this? Well, it's fairly simple. Let's say I have two points, P and Q, on this elliptic curve. In order to add them together, I simply draw a line through P and Q. Lastly, I take the third point on the curve which the line intersects, and then I reflect that point across the x-axis. Let's call this new point R. P + Q = R.

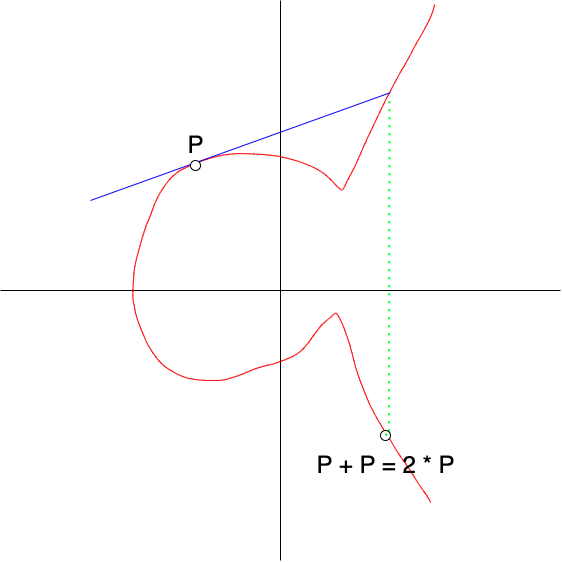
Cool, so now we know how to add two points on an elliptic curve. How do we start doing cool things? Well, one last thing. What if I wanted to add P to itself? We didn't really cover that. If we tried to do what we did in the above example and try to draw a line that intersects P, and... P? Well there are infinitely many lines which do that. Ah, but what if we drew a line tangent to P? There's only one such line which is tangent to P, and then we can just do the same trick we did above, we draw a line tangent to P, find where it intersects on the curve, and then reflect that point across the x-axis, and that's P + P, or 2•P. We can keep doing this if we want, we can find P + P + P or 3•P by just by just drawing a line through P and 2•P, finding the third spot it intersects the curve, and reflecting it across the x-axis. So 3•P = P + P + P = 2•P + 1•P.
What if I wanted to calculate 10•P? How many point additions do I need to do? You might think it's 9, since P + P + P + P + P + P + P + P + P + P would require 9 point additions but if you think about it we can actually cheat a bit. Just like above, where 3•P was equal to P + P + P which was equal to 2•P + 1 • P, to generalize, n•P + r•P = (n + r) • P, so the fastest way I can calculate 10•P isn't by doing 9 separate point additions, but instead by calculating the following:
P + P = 2•P
2•P + 2•P = 4•P
4•P + 4•P = 8•P
10•P = 2•P + 8•P
That's a pretty nice improvement; we only had to do 4 point additions instead of 9. Now here's a tough question, how many point addition operations would we have to do in order to calculate x•P, where x is some random 256-bit number? If we did it the crappy way it would take longer than the age of the universe to do because we'd have to do at most something like 2256 - 1 point additions, but incredibly we can do it in a maximum of 510 point additions. The difference of scale in these numbers is incredible. One is a fairly close estimate to the number of atoms in the universe and the other is, well 510. So what magic is at work here? Well, we've got a trick up our sleeve.
We start by computing the series 20 • P, 21 • P, 22 • P, 23 • P, ..., 2255 • P. That only takes 255 point additions because there are 256 points and you can get from one point to the next by just adding the current point to itself since 2n•P + 2n•P is just 2n + 1•P, or in other words, to get 2255 • P, if I already have 2254 • P, I can just add 2254 • P and 2254 • P. So basically we do this whole mess once which takes us 255 point additions. Well I said it was going to take at most 510 point additions? Where are the missing 255?
Well, now we can just represent our x through binary expansion. Let's say x is 42. Well that's just 25 + 23 + 21, 32 + 8 + 2 = 42. Now we just multiply that binary expansion by P, so 25 • P + 23 • P + 21 • P = 42 • P, and since we already pre-calculated that series we don't have to do 41 point additions on top of the 255 we did before, we just have to do 2. Since the binary expansion of a 256 bit number can have at most 256 elements, this last step will never require more than 255 point additions. So pre-calculating the series took us 255 point additions, and then the max the binary expansion of x can take is another 255 point additions for a total of 510 point additions.
Alright, so we can add points on an elliptic curve together and it would seem we can calculate x • P where x is some massive 256 bit number fairly quickly, big whoop. When do I get to cool billion dollar problems? Well, on the secp256k1 curve there is a special point P known as the base point. There's nothing particularly special about it, but we just wanted to define some point which everyone can use as a basis for beginning our actual cryptography. That base point is x-coordinate: 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798 and y-coordinate: 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8.
If you generate some 256 bit random number, x and multiply it with the base point P (which will take you at most 510 point addition operations), it will result in some new point X. What about reversing that? If I gave you X and you knew the base point P, how long would it take you to calculate that random 256 bit number x? The answer, so far as any of us can tell, is longer than the age of the universe1.There is no known algorithm better than brute force which would on average require you to do 2128 point additions which even with all the computing power currently on Earth would take you longer than the age of the universe. This is the discrete log problem (well, technically the discrete log problem is solving this over the discrete curve y2 mod p = (x3 + ax + b) mod p where p is prime; for secp256k1 it's the largest prime that is smaller than 2256), and it's the foundation for all modern cryptography including cryptocurrency. The 256 bit random number x is your private key. The resulting point from doing a relatively small number of point additions is a point representing your public key X, and your address on the Blockchain is just the result of doing some operations which vary by Blockchain on that point X. Specifically, for Ethereum, we would run that point X through a keccak256 hash, take the last 40 bytes, and throw a 0x in front of it, and bam, that's your wallet address.
This is the problem that, if solved, would instantly make you a billionaire. Calculating a 256 bit number • P resulting in some point X? Your phone can do that in a second. Trying to figure out that 256 bit number given P and that point X? All the computing power on Earth and it would take longer than the age of the universe. But again, is the reverse (the discrete log problem) actually that much more difficult than point addition? Is factoring a large semiprime into its two prime factors actually more difficult than multiplying two prime numbers together? (This is actually what RSA relies on). Does P == NP? No one knows. Billions of dollars and all privacy on the Internet relies on the fact that so far all the smartest people in the world haven't been able to think of a good way to approach the discrete log problem, but critically, there is no proof whatsoever that this problem is actually difficult. So maybe take a few minutes today and think about it. At worst, you'll waste a couple minutes, but hey, if you stumble upon some kind of trick you'll become a billionaire overnight.
If you liked this little presentation, I'm considering doing a follow-up which builds on this one, which involves proving that you know x while revealing no actual information about x. This is important because it lets us do things like sign messages and prove to others in a way that is quick to verify that we must know x while leaking no actual information about what x is.
If you found any of this helpful, feel free to send me some dust at lutzy.eth!